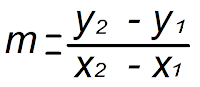SISTEMA DE ECUACIONES LINEALES

ECUACIÓN 

Una ecuación es un enunciado que declara la igualdad de dos expresiones.  Escribimos una ecuación poniendo el signo de igualdad, “=”, entre las dos expresiones. Ejemplos:

5 = 3 + 2             3x + 1 = 7 + y            2x = x + 1           2(3x +1) - 4 = 6x – 2

ECUACIÓN LINEAL

Pero en este momento a nosotros nos interesan solo las ecuaciones lineales. Ahora recordemos que toda ecuación de la forma ax + by = c (Ecuación General de la Recta) o      y = mx + b (Ecuación Canónica) es una ecuación lineal

SISTEMA DE ECUACIONES LINEALES

En matemáticas y álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales sobre un cuerpo.

Por lo tanto para que sea un sistema lineal se necesitan mínimo dos ecuaciones lineales. Un ejemplo de sistema lineal de ecuaciones sería el siguiente:

Una ecuación lineal con dos incógnitas representa una recta en el plano cartesiano, de modo que un sistema de dos ecuaciones permite una representación gráfica como dos rectas en el plano cartesiano, siendo la solución al sistema el punto de intersección de estas dos rectas.

Ejemplo: consideremos el siguiente sistema.

Si en estas ecuaciones despejamos la y, obtenemos su forma explícita o canónica:

Estas dos rectas se cortan en el punto:

Esta es la grafica de este sistema lineal

TIPOS DE SOLUCIÓN

En un sistema de ecuaciones se pueden dar los siguientes casos:

Sistema compatible: si admite soluciones

·   Sistema compatible determinado: si admite un número finito de soluciones; en el caso de dos ecuaciones lineales con dos incógnitas, si el sistema es determinado solo tendrá una solución. Su representación gráfica son dos rectas que se cortan en un punto; los valores de x e y de ese punto son la solución al sistema.

·  Sistema compatible indeterminado: el sistema admite un número infinito de soluciones; su representación gráfica son dos rectas coincidentes. Las dos ecuaciones son equivalentes y una de ellas se puede considerar como redundante: cualquier punto de la recta es solución del sistema.

Sistema incompatible: el sistema no admite ninguna solución. En este caso,

       su representación gráfica son dos rectas paralelas y no tienen ningún punto

       en común porque no se cortan. El cumplimiento de una de las ecuaciones

       significa el incumplimiento de la otra y por lo tanto no tienen ninguna solución

       en común.

Partiendo de los conceptos anteriores y del siguiente ejemplo vamos a ver las formas básicas de resolver dos ecuaciones lineales con dos incógnitas.

Ejemplo 1 Dos empresas de telefonía celular  facturan así:

Empresa 1: $ 200 por cada minuto y una cuota fija de $ 4.000

Empresa 2: $ 100 por cada minuto y una cuota fija de $ 4.500

Si se consumen pocos minutos la factura de la empresa 1 tendrá menos valor y si el consumo es mucho mayor la factura de la empresa 2 tendrá el menor valor. Pero en algún punto intermedio las dos empresas tendrán una facturación igual, ¿Cuál será ese punto?

Solución:

Observemos que las ecuaciones canónicas son:

Empresa 1: 200X + 4.000

Empresa 2: 100X + 4.500

Lo que nos da el siguiente sistema de ecuaciones, de dos ecuaciones (1) y (2) con dos incógnitas ( X y Y ).

Si el sistema anterior es compatible y determinado, entonces resolver el sistema consiste en encontrar los valores de x y de y que satisfacen las dos ecuaciones simultáneamente.

Podemos diferenciar tres tipos de métodos de resolución de sistemas de ecuaciones: el grafico, los básicos (basados en operaciones algebraicas encaminados a despejar el valor de cada una de las incógnitas) y los avanzados (basados en propiedades de los sistemas que determinan los distintos valores de las incógnitas que cumplen las ecuaciones del sistema).

Veamos ahora el primer método.

MÉTODO 1: GRAFICO

Una vez planteado el sistema de ecuaciones procedemos a elaborar una tabla de valores correspondiente a cada función y luego la graficamos, así:

X	0	1	2	3	4	5	6	7
Y = 200X + 4.000	4.000	4.200	4.400	4.600	4.800	5.000	5.200	5.400
Y = 100X + 4.500	4.500	4.600	4.700	4.800	4.900	5.000	5.100	5.200

Graficamos Las dos funciones lineales en un solo plano cartesiano, tenemos:

Como vemos las dos rectas se cortan en x = 5  y  para el cual las dos empresas facturan lo mismo  Y = 5.000. La solución del sistema de ecuaciones lineales es ( 5 , 5.000 ).

Próximamente publico los otros metodos.

ECUACIÓN DE LA RECTA DADOS DOS PUNTOS

Dados dos puntos de la recta (punto 1(x1,y1) y punto 2 (x2,y2)) podemos encontrar la ecuacion de la recta o funcion lineal

Lo primero es hallar la pendiente de la recta (m) utilizamos la formula

Donde x1 y y1 son las coordenadas del punto uno (1) y x2 y y2 las coordenadas del punto dos (2).

Después encontramos el valor de b, una vez se remplace m en la ecuación sustituimos los valores de x y de y por los valores de las coordenadas de uno de los puntos, sea el uno o el dos, el que ustedes deseen, y despejamos b para así obtener su valor.

Ejemplo 1 Una empresa que presta el servicio de gas tiene una cuota fija por servicio, además cobra cierto valor por metro cubico consumido. Si por 25 m³ cobran $ 22.000 y por 32 m³ $ 27.600, encontrar el valor del metro cubico consumido y la cuota fija.

Solución:

Hallamos el valor de la pendiente de la recta (m).

Para esto definimos los puntos, el punto uno (1) es ( 25 , 22.000 )
                                            y el punto dos (2) es ( 32 , 27.600 )

  

  Por lo que   m = 800

Ahora con la ecuación canónica y el valor de m obtenemos el valor de b.

y = mx + b                  m = 800

y = 800x + b               ecuación (A)

Tomamos un punto ya sea ( 22 , 22.000 ) o ( 32 , 27.600 ) (yo tomare el primero pero tú puedes usar cualquiera de los dos), y los remplazo por x y y en la ecuación (A) quedándome:

        y  =  800 x    + b

22.000 =  800(22) + b                 realizando la multiplicación de 800x22 nos queda

22.000 =  20.000  + b                 y despejando b tenemos

b = 22.000 – 20.000 = 2.000      b = 2.000

De lo anterior tenemos que m = 800 y b = 2.000, quedando la ecuación canónica así:

y = 800X + 2.000. El valor del metro cubico de gas es de $ 800 y la cuota fija de $ 2.000.

Si queremos hacer la grafica (en el plano cartesiano) de la función tomamos los dos puntos dados y los ubicamos así:

Ejemplo 2 En las 10 primeras semanas de cultivo de una planta, que medía 2 cm al comenzar, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en la primera semana ha pasado a medir 2.5 cm. Establecer una función a fin que dé la altura de la planta en función del tiempo y representar gráficamente.

Este ejemplo tengo pensado subirlo en vídeo, al hacerlo les pongo el enlace.

Aquí otro vídeo interesante, en el cual les muestran dos ejemplos, en el primero les dan un punto y la pendiente m y en el segundo les dan los dos puntos.

FUNCIÓN LINEAL "APLICACIONES"

TEMA ANTERIOR

z  Observa cómo se resuelven los siguientes ejercicios:

1. Un algodonero recoge 30 Kg cada hora, y demora media hora preparándose todos los días cuando inicia la jornada. La función lineal que representa esta situación es y = 30x – 15 donde y representa los Kg de algodón recogido y x el tiempo transcurrido en horas.

Realiza una tabla para la anterior función y grafícala.

¿Cuantos Kg de algodón se recogerán en una jornada de 8 horas?

Solución:

Primero realizamos la tabla.

x (tiemp en horas)	y (Kg algodón)
0.5	0
1	15
1.5	30
2	45

 y luego graficamos

Si tienes problemas para realizar la tabla repasa los vídeos en la publicación anterior.

Ahora para saber cuanto algodón se recoge en 8 horas:

y = 30x – 15    para x = 8 necesitamos hallar el valor de y

para eso remplazamos a la x por su valor que es 8 y nos queda


y = 30(8) – 15 = 240 - 15 = 225    (recuerda que 30(8) es un producto)
y = 225 Kg


La cantidad de algodón recogido en ocho horas es de 225 kg

2. Por el alquiler de un coche cobran una cuota fija de 20.000 pesos y adicionalmente 3.000 pesos por kilómetro recorrido. Escribe la ecuación canónica que representa esta función y grafícala, ¿cuánto dinero hay que pagar para hacer un recorrido de 125 Km? y si page un valor de 65.000 pesos ¿cuantos quilómetros recorrí?


Solución:

Primero definimos cual es la ecuación para esto tenemos en cuenta esto:

Importante: Para resolver este tipo de problemas donde nos piden hallar el valor por unidad consumida y la cuota fija usaremos la ecuación canónica, donde la pendiente de la recta (m) es siempre el valor por unidad consumida y b la cuota fija.

Así m será 3.000 que es el valor por unidad (kilometro recorrido) y b es 20.000 que es la cuota fija, quedando la ecuación y = 3.000x + 20.000, ahora podemos realizar la tabla.

X (Km recorrido)	y (Valor a pagar)
0	20.000
10	50.000
20	80.000
30	110.000

Con esto la grafica nos queda así:

·    Para saber cuánto nos cuesta un recorrido de 125 Km usamos la ecuación lineal y cambiamos la variable x por el valor de 125 Km, así:

y = 3.000(125) + 20.000 = 375.000 + 20.000 = 395.000

y = 395.000

El valor en pesos a pagar por un  recorrido de 125 Km es de 395.000 pesos.

·        En este caso nos dan el valor de y (valor a pagar 65.000 pesos) y nos piden hallar el de X (kilometraje recorrido) podemos hacerlo de dos maneras.

La primera: remplazamos el valor de y en la ecuación, de lo que obtendremos.

65.000 = 3.000X + 20.000  despejando x nos queda.

65.000 – 20.000 = 3.000X        45.000 = 3.000X        45.000/3.000 = X

X = 15

La segunda: graficamos la función y cómo podemos ver en la grafica, para un valor de y igual a 65.000 tenemos un valor de X igual a 15

El kilometraje recorrido por el cual pagamos 65.000 es 15 Km.

FUNCIÓN LINEAL

Una función lineal es una función cuyo dominio son todos los números reales, cuyo codominio también todos los números reales, y cuya expresión analítica es un polinomio de primer grado.

La función lineal se define por la ecuación f(x) = mx + b ó y = mx + b llamada ecuación canónica, en donde m es la pendiente de la recta y b es el intercepto con el eje Y.

Por ejemplo, son funciones lineales f(x) = 3x + 2 g(x) = - x + 7 h(x) = 4 (en esta m = 0 por lo que 0x no se pone en la ecuación).

Esta es la gráfica de la función lineal y = 3x + 2

Vemos que m = 3 y b = 2 (de la forma y = mx + b)

Este número m se llama pendiente de la recta y es la relación entre la altura y la base, aquí vemos que por cada unidad recorrida en x la recta sube 3 unidades en y por lo que la pendiente es m = 3. & b es el intercepto de la recta con el eje Y (donde la recta se cruza con el eje Y)

Volvamos al ejemplo de las funciones lineales

f(x) = 3x+2       Si x es 3,  entonces f (3) = 3*3+2 = 11

Si x es 4,  entonces f (4) = 3*4+2 = 14

Si x es 5,  entonces f (5) = 3*5+2 = 17

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, f(x), se incrementa en 3 unidades. Si el valor de la pendiente es positivo la función es Creciente. Preste atención en que los valores de   x  y de  f(x)  NO SON PROPORCIONALES.

Lo que son proporcionales son los incrementos.

g(x) = -3x+7     Si  x= 0, entonces g (0) = -3*(0) +7 =   0+7 = 7

Si  x= 1, entonces g (1) = -3*(1) +7 = -3+7 = 4

Si  x= 2, entonces g (2) = -3*(2) +7 = -6+7 = 1

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, g(x), disminuye en 3 unidades. Si el valor de la pendiente es negativo la función es Decreciente.

h(x) = 4             Si  x= 0   ,  entonces h(0)  = 4

Si  x= 98   entonces h(98) = 4

Cada vez que la x se incrementa en 1 unidad, el resultado, esto es, h(x), NO aumenta. Es la función constante. Su gráfica es una recta paralela al eje X.

Esta es la representación grafica de los tres tipos de funciones descritas.

Si quieres ampliar estos conceptos te recomiendo estas paginas:

http://es.wikipedia.org/wiki/Funci%C3%B3n_lineal

http://www.x.edu.uy/lineal.htm

http://www.ing.unp.edu.ar/matematica/Modulos/Unidad_4.PDF

Ahora veamos como graficar una función.

z Ejemplos

Representa gráficamente las siguientes funciones lineales  y = 2x  y  y = - 3x + 4

Sugerencia: Primero elabora una tabla de valores, luego ubica los pares de puntos de la tabla en el plano cartesiano y finalmente únelos con una línea recta.

Los valores de x son asignados arbitrariamente o a tu gusto "te aconsejo usar valores pequeños para facilitar las operaciones" luego en la ecuación remplazamos la x por cada valor de la tabla. 

1.       y = 2x
Vamos a hacerlo con dos valores de x para que sepas de donde salen los valores.

       Para x = - 2, y = 2(-2) = -4  quedando la pareja (-2 , -4)

       Para x =  1,  y = 2(1)  =  2   quedando la pareja (1 , 2)

X	y = 2x
-2	-4
-1	-2
0	0
1	2
2	4

2.       y = - 3x + 4
Vamos a hacerlo con dos valores de x para que sepas de donde salen los valores.

       Para x = - 1, y = -3(-1)+ 4 =  7  quedando la pareja (-1 , 7)

       Para x =  2,  y = -3(2) + 4 = -2   quedando la pareja (2 , -2)

X	y = - 3x + 4
-1	7
0	4
1	1
2	-2
3	-5

Si tienes dudas de como graficar una función lineal te recomiendo estos vídeos:

Esta es otra forma de graficar una función lineal:



SI QUIERES SABER MAS CONTINUA AQUI