Dados dos puntos de la recta (punto 1(x1,y1) y punto 2 (x2,y2)) podemos encontrar la ecuacion de la recta o funcion lineal
Lo primero es hallar la pendiente de la recta (m) utilizamos la formula
Después encontramos el valor de b, una vez se remplace m en la ecuación sustituimos los valores de x y de y por los valores de las coordenadas de uno de los puntos, sea el uno o el dos, el que ustedes deseen, y despejamos b para así obtener su valor.
Ejemplo 1 Una empresa que presta el servicio de gas tiene una cuota fija por servicio, además cobra cierto valor por metro cubico consumido. Si por 25 m3 cobran $ 22.000 y por 32 m3 $ 27.600, encontrar el valor del metro cubico consumido y la cuota fija.
Solución:
Hallamos el valor de la pendiente de la recta (m).
y el punto dos (2) es ( 32 , 27.600 )
Por lo que m = 800
Ahora con la ecuación canónica y el valor de m obtenemos el valor de b.
y = mx + b m = 800
y = 800x + b ecuación (A)
Tomamos un punto ya sea ( 22 , 22.000 ) o ( 32 , 27.600 ) (yo tomare el primero pero tú puedes usar cualquiera de los dos), y los remplazo por x y y en la ecuación (A) quedándome:
y = 800 x + b
22.000 = 800(22) + b realizando la multiplicación de 800x22 nos queda
22.000 = 20.000 + b y despejando b tenemos
b = 22.000 – 20.000 = 2.000 b = 2.000
De lo anterior tenemos que m = 800 y b = 2.000, quedando la ecuación canónica así:
y = 800X + 2.000. El valor del metro cubico de gas es de $ 800 y la cuota fija de $ 2.000.
Si queremos hacer la grafica (en el plano cartesiano) de la función tomamos los dos puntos dados y los ubicamos así:
Ejemplo 2 En las 10 primeras semanas de cultivo de una planta, que medía 2 cm al comenzar, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en la primera semana ha pasado a medir 2.5 cm. Establecer una función a fin que dé la altura de la planta en función del tiempo y representar gráficamente.
Este ejemplo tengo pensado subirlo en vídeo, al hacerlo les pongo el enlace.
Aquí otro vídeo interesante, en el cual les muestran dos ejemplos, en el primero les dan un punto y la pendiente m y en el segundo les dan los dos puntos.
Aquí otro vídeo interesante, en el cual les muestran dos ejemplos, en el primero les dan un punto y la pendiente m y en el segundo les dan los dos puntos.

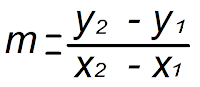


HODA, MUY BIEN EXPLICADO HODA
ResponderEliminar800 * 22 no es igual a 20,000, por lo tanto el problema no esta bien.
ResponderEliminarEso confunde mas
Eliminarel resultado es correcto ya que se equivoco al poner el numero ya que era 25*800 y eso da 20000
EliminarLuego del cálculo de la pendiente figura erróneamente el valor 22 en lugar de 25 que es el que se especifica en el problema. Verificación 800 * 25= 20000
ResponderEliminarMariel
mal
ResponderEliminarmal
ResponderEliminarHola alguien me puede explicar el final de la ecuación que he visto que se ha escrito mal esta y me gustaría que alguien me ayudara en este tema
ResponderEliminarmal
ResponderEliminarmal
ResponderEliminarEl que...
ResponderEliminarEl que???
7 pollo
Hola, muchas gracias por la explicación, tan lindos todos ustedes, los amo bye
ResponderEliminarte equivocaste loco pusiste 22 y era 25
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarMe puede ayudar con este trabajo
ResponderEliminarHallar la dependiente de la recta q posa por cada par de punto
(1_2,4)y(-4,5)